Basic Theory of Discretization Errors by Determining Area, Volume, and Mass Moments of Inertia
by
© Ph. D. & Dr. Sc. Lev Gelimson
Academic Institute for Creating Fundamental Sciences (Munich, Germany)
RUAG Aerospace Services GmbH, Germany
Mechanical and Physical Journal
of the “Collegium” All World Academy of Sciences
Munich (Germany)
6 (2006), 1
By calculating area, volume, and/or mass and moments of inertia, integration provides the exactness of their values. Discretizing the areas, volumes, and/or masses and choosing suitable approximations to them and to the coordinates of their centroids (centers of area/volume/mass/gravity) lead to discretization errors to be estimated. Consider that it is possible to provide approximation error as small as required by suitably triangulating each area practically relevant even by using right triangles only whose each cathetus is parallel to one of the axes. Hence it is sufficient to consider the area moments of inertia only of such a triangle with constant thickness. By three-dimensional objects with variable thickness, simply use such triangular ”sheets” whose numbers vary along conventional lengths and/or widths. To show result invariance by changing the position of such a right triangle, consider a coordinate system one of whose axes contains one cathetus, the hypotenuse dividing the first quadrant at the system origin, as well as the central coordinate system with the axes parallel to the above ones. To obtain the lower and upper bound of the order of the corresponding discretization errors, subsequently choose all the approximations from below and above, respectively. Adding an adjacent rectangle to such a right triangle brings no additional absolute error and therefore decreases the relative error and provides strong estimates.

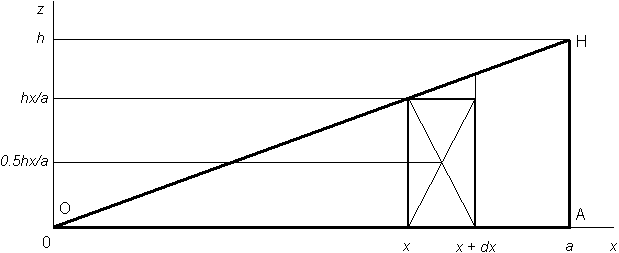
Here dx denotes the differential of x. For the area moments of inertia Ix and Iz of right triangle OAH with base a and height h about axes 0x and 0z, integration [1] brings the exact results:
Ix = ∫0a (hxdx/a) (0.5 hx/a)2 = 0.25 h3/a3 ∫0a x3 dx = ah3/16,
Iz = ∫0a (hxdx/a) x2 = h/a ∫0a x3 dx = a3h/4.
In a similar figure (not shown) for lower-bound estimating discretization error, the symbol n denotes the (finite) cardinal number of the parts of side OA and thus of the right triangle OAH due to the corresponding vertical lines whereas k varies from 0 to n - 1 indicating the ordinal number of the part containing the interval between ak/n and a(k + 1)/n. Replace the area of the kth (trapezoidal) part with the smaller rectangle, take the (smaller) ordinate of the rectangle centroid by calculating Ix, and replace the abscissa of the rectangle centroid with the smaller value ak/n by calculating Iz . Direct summation brings the following lower-bound estimates:
Ix = Σ0n-1(a/n)(hk/n)(0.5hk/n)2 = 0.25ah3/n4Σ0n-1k3 = 0.25 ah3/n4 ((n-1)n/2)2 = (1-1/n)2 ah3/16,
Iz = Σ0n-1(a/n)(hk/n)(ak/n)2 = a3h/n4 Σ0n-1k3 = a3h/n4 ((n - 1)n/2)2 = (1 - 1/n)2 a3h/4
with multiplying their exact values by (1 - 1/n)2 = 1 - 2/n + 1/n2. By n great enough (e.g., 100 by the order of value), 1/n2 is very small and can be omitted. In such a case the factor is about 1 - 2/n and the relative error is about 2/n, as well as by central axes.
By upper-bound estimating discretization error, replace the area of the kth (trapezoidal) part with the greater (shown) rectangle, take the greater ordinate of the rectangle centroid by calculating Ix , and replace the abscissa of the rectangle centroid with the greater value a(k + 1)/n by calculating Iz . Then direct summation brings the following upper-bound estimates:
Ix = Σ0n-1(a/n)(h(k + 1)/n)(0.5 h(k + 1)/n)2 = 0.25 ah3/n4 Σ0n-1(k + 1)3 = (1 + 1/n)2 ah3/16,
Iz =Σ0n-1(a/n)(h(k +1)/n)(a(k +1)/n)2 =a3h/n4Σ0n-1(k +1)3 = a3h/n4(n(n +1)/2)2 = (1+1/n)2 a3h/4
with multiplying their exact values by (1 + 1/n)2 = 1 + 2/n + 1/n2. By n great enough (e.g., 100 by the order of value), 1/n2 is very small and can be omitted. In such a case the factor is about 1 + 2/n and the relative error is about 2/n , as well as by central axes. We see this value is universal. By three-dimensional discretizing (with n1 , n2 , and n3 great enough, e.g., 100 by the order of value) the object to be considered, the relative error is about 2(1/n1+ 1/n2 + 1/n3) and this value is universal, too. Hence by estimating area, volume, and mass moments of inertia [2-4] about both central and noncentral axes with using adequate discretization of objects, any method of reasonably choosing the values of the areas, volumes, and masses of elements, as well as the coordinates of their centroids, leads to results with relative errors small enough.
[1] Encyclopaedia of Mathematics. Ed. M. Hazewinkel. Vols. 1 to 10. Kluwer Academic Publ., Dordrecht, 1988-1994
[2] Handbuch Struktur-Berechnung. Prof. Dr.-Ing. L. Schwarmann. Industrie-Ausschuss-Struktur-Berechnungsunterlagen, Bremen, 1998
[3] Lev Gelimson. Elastic Mathematics. General Strength Theory. The ”Collegium” International Academy of Sciences Publishers, Munich (Germany), 2004
[4] Elementos de resistencia de materiales; por S. P. Timoshenko y D. H. Young; traducción de Jesús Ibáñez Gar. 2ª ed. Barcelona: Montaner y Simón, DL 1979